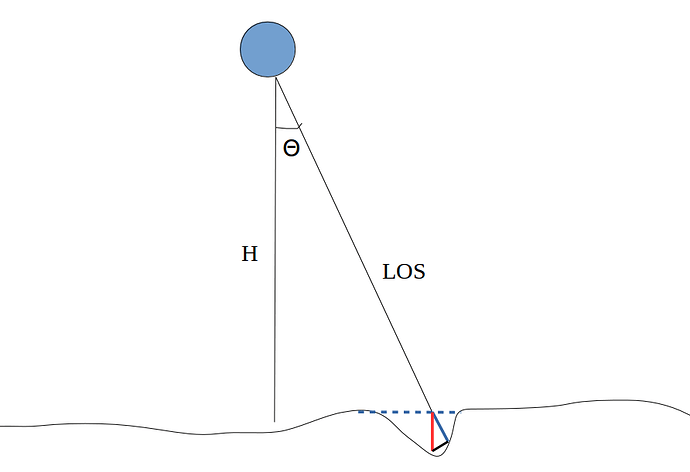
Hi,
Below, i tried to sketch the relationship between LOS and vertical displacement (not the ideal diagram though). In order to find the real displacement, we need to do some geometrical calculations between the incidence angle and the direction of the ground movement. In the (beautiful 
) diagram below, the blue line denotes the LOS displacement and the red line the vertical displacement (this is what we are trying to find.).
using your formula vert_disp = (unwrapped phase * wavelenght*cos(rad(incidence angle)))/ (-4pi ) the results we get are much smaller compared to the following formula (unwrapped phase * wavelength) / (-4 * PI * rad(cos(incidence angle))). If the ground in your area of interest has moved vertically(we must assume that the horizontal component is zero) , then the vertical displacement values should be bigger compared to that of LOS.
You can have a look at the following website (https://vldb.gsi.go.jp/sokuchi/sar/mechanism/mechanism04-e.html) where after ALOS measurements, they found out that the amount of subsidence is 1.3 times the amount of deformation in LOS direction.
In order to validate this equation, the only way is to have precise GPS measurements over your area of interest and compare the GPS results with your vertical displacement map. As long as scientists use the following equation (unwrapped phase * wavelength) / (-4 * PI * rad(cos(incidence angle))), then that means that the equation was validated and produces the expected results.