This is a similar thread to DaveRose’s from 2016.
I have written a remedial Sentinel-1 Level-0 IW image formation tool in a mix of Matlab and C/mex files. My tool reads the raw L0 data (both the aux info and pulse samples), groups the data into bursts, and forms image chips for each burst. It can process an entire Level-0 file into the associated burst image chips. I need to be able to access the data at every step of the image formation process to be able to inject various types of processing that are most efficient in the different domains accessed.
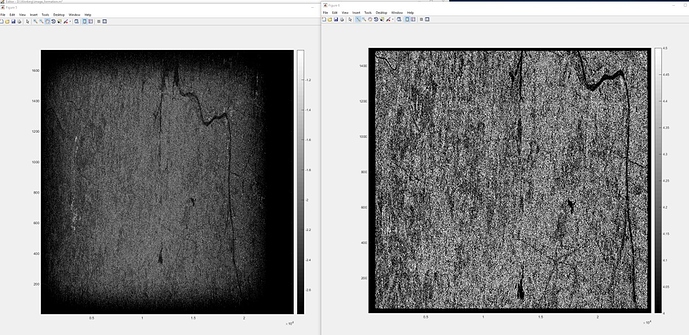
This image shows a poor resolution representation of my results. My formed (detected) image is on the left. I fade to black at the edges because I am trying to process the full collected extent. As the numerical/spectral support tapers off (to 0 from my padding to avoid further frequency wrapping), the output/formed energy tapers off (to 0) as well. The ‘same’ ESA-formed L1 SLC burst (detected) image is on the right.
I am currently having several problems, though dominated by two areas - mapping formed pixels to ground locations and matching some of the derived formation values defined in “Sentinel-1-Level-1-Detailed-Algorithm-Definition.pdf” (and associated ESA documentation).
Although “Sentinel-1-Level-1-Detailed-Algorithm-Definition.pdf” defines some of the pointing in section 5.1, there is a disconnect in the definition and implementation of the quaternion values. I get different Q0-Q3 values from the L0 raw versus what is published in the same collect/product L1 SLC annotation XML. The PDF defines obtaining some vectors through the use of pitch, roll, and yaw - relate-able to Q0-Q3, but does not actually give an example of the math/process applying the recorded quaternions. Worse, I can not find any way to map from the SLC XML Q0-Q3 to the pitch, roll, and yaw in the same ‘attitude’ section of the XML. (RESOLVED at https://www.researchgate.net/post/Can_someone_explain_the_Sentinel-1_orientation_quanternion_vs_pitch_roll_yaw_numbers_to_me) Does anyone have a write-up or example that walks through the pointing steps using quaternions? (Not resolved…)
(Based on the algorithms and variable definitions in Sentinel-1-Level-1-Detailed-Algorithm-Definition.pdf) In the formation process, there are a number of values that are very important to get right (or at least ‘accurate-ish’) in the frequency unwrapping and the azimuth compression. Although I can get a good approximation of ks, I am having trouble nailing down ka. ka becomes important for my calculation of Ns (duplications of the initial spectrum in the frequency unwrap) and my subsequent deramp and reramp of data. The key function D(f_eta,Vr), (and its details I’m not getting right enough) impact the azimuth compression by skewing the numbers in my formation of the azimuth matched filter. I think I need to resolve the pointing issues/math before I can nail ka, Ns, and D. Has anyone been able to get accurate ka, Ns, and D function approximations without working out all the details of the pointing vectors?
I am happy to make technical exchange for useful, constructive discussion. Please don’t leave answers that say s1tbx does not do image formation (got it!), or that I should look at the documents on the ESA web site (done - referenced above). I have similar threads running on ResearchGate, but haven’t gotten as much response as I expect to get from this Sentinel-1 dedicated forum.