I read that statement in Andrew Hooper’s 2004 research about testing PSI in Measuring deformation on valcanoes. It’s the method upon which the persistent scatter pixels are selected for Interferometric time series based on thresholding their amplitudes dispersion over time. However, I could quite understand the mechanism.
amplitude dispersion is the amplitude standard deviation divided by the mean amplitude.
This means, a pixel which has a constant value over the entire period (e.g. a building or bare soil) has a low standard deviation and therefore a small dispersion. If it changes its backscatter intensity over time (e.g. agriculture, water, forest), the standard deviation is high which makes the dispersion large.
Amplitude dispersion is therefore an easy to calculate indicator for the stability of a pixel.
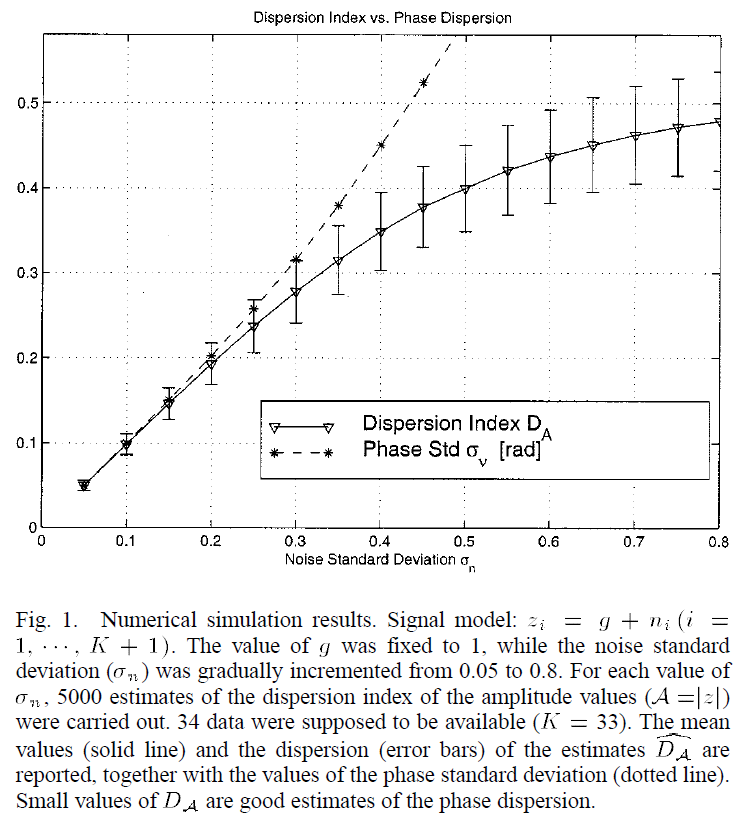
Low amplitude dispersion at high SNR values are optimal for phase dispersion estimation. But I don’t quite understand from a statistical point of view or from wave-physics perspective, how is the amplitude dispersion over time related to the phase measurements from persistent scatterers according to this figure from Ferretti and Rocca 2001
Additionally, are the persistent scatterers selected from coherence maps and the interferograms altogether ?