Hello again dear @ABraun!
Thank you for your reply, it was a big read the last post.
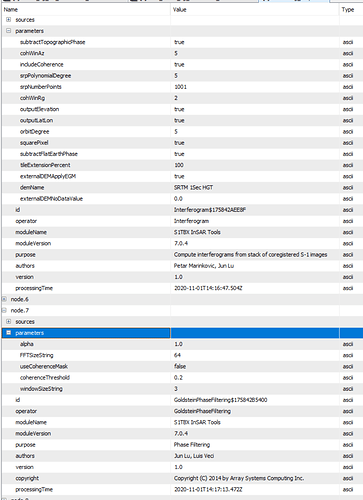
I did what is mentioned there with the parameters and I got rid of those slow varying waves of the interferograms. (by increasing the flat earth orbit degree)
I also did that with DEM assisted coregistration, which resulted in non varying waves in phase.
Below is the parameters used for the interferogram:
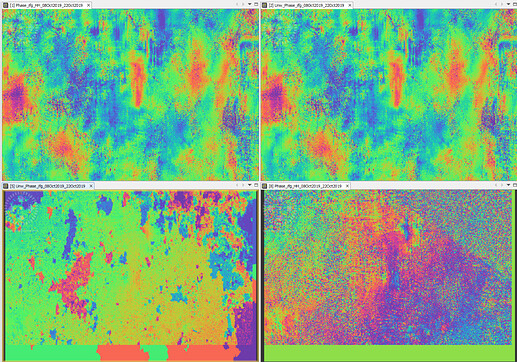
Here are some results (same pair as previous post, different arbitrary subset):
Top: Coregistration: Create Stack
Left: Filter G/S Wrapped phase
Right: Filter G/S Un-wrapped phase
Bottom: Coregistration: DEM-Assisted
Left: Filter G/S Un-wrapped phase
Right: Filter G/S Wrapped phase
I have also translated them into displacement, as you can see bolow:
Left: Create Stack + Coherency>0.5
Right: DEM-Assisted + Coherency>0.5
The low coherence on the right makes me unease with DEM-Assisted cor.
(How am I supposed to evaluate this based on: (Interferogram from Alos palsar 1.1 data) ?)
The left displacement image makes some sense. However, if you look at the first figure, the wrapped and unwrapped interferograms look the same. The only difference I observe is that the wrapped ranges in [-π, +π] while the unwrapped ranges in [-2π, +2π]
At the end though, how am I to be sure to extract the ionospheric effect so that the remainder is the actual subsidence?