In order to test if different polarizations interfere in multi-temporal speckle filtering I made the following tests:
I downloaded 11 Sentinel-1 images in dual polarization (VH VV), applied orbit files and coregistered them.
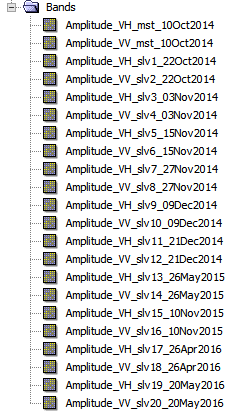
As you can see, the temporal range is about 1.5 years. Unfortunately, the data is not evenly distributed over the given time span. I therefore used 03.11.14 / 15.11.14 and 27.11.14 for RGB image as they had the smallest temporal baseline.
The following results show:
- Unfiltered data
- Multi-temporal filter on VH data only
- Multi-temporal filter on VV data only
- Multi-temporal filter on both VH and VV data (VV-RGB is shown)
Filter size was 3x3, I used the Quegan filter from the NEST toolbox.
First comparison doesn’t show much difference:
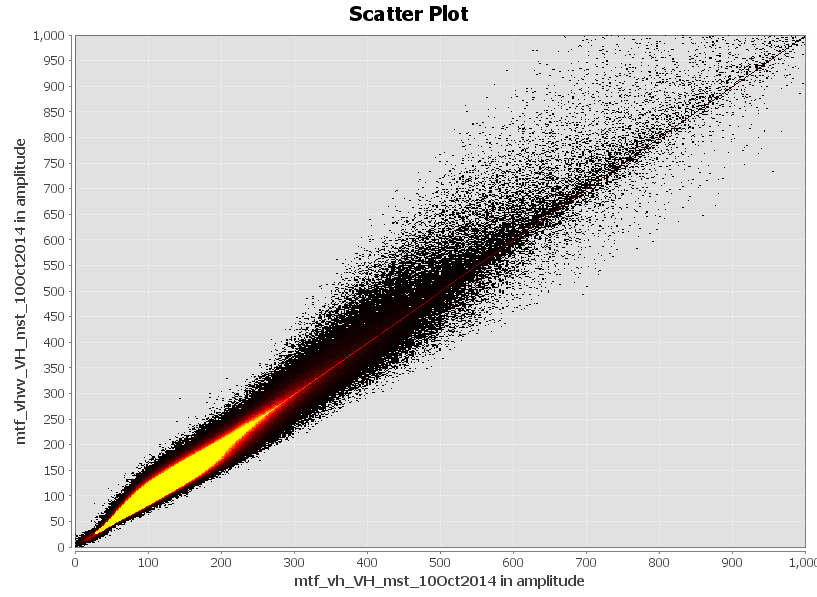
I then made a crosstable between the data sets from 10.10.14 to see how similar they are:
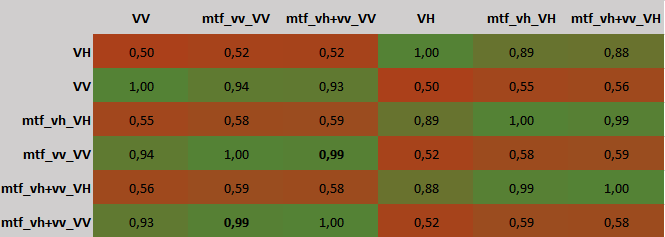
It shows that the results of single-polarization filtering (mtf_vv_VV) are nearly the same (bold r² = 0.99) as the results from dual-polarization filtering (mtf_vh+vv_VV). . In turn, the correlation of unfiltered data (VV) to filtered (mtf_vh+vv_VV) is clearly smaller (r² = 0.93). These numbers give a small idea of the differences between unfiltered, single-polarization filtered and dual-polarization filtered data but cannot explain the spatial dimension. 1% in a 5000x6000 pixel subset is about 300000 pixels (compared to 3 million in total).
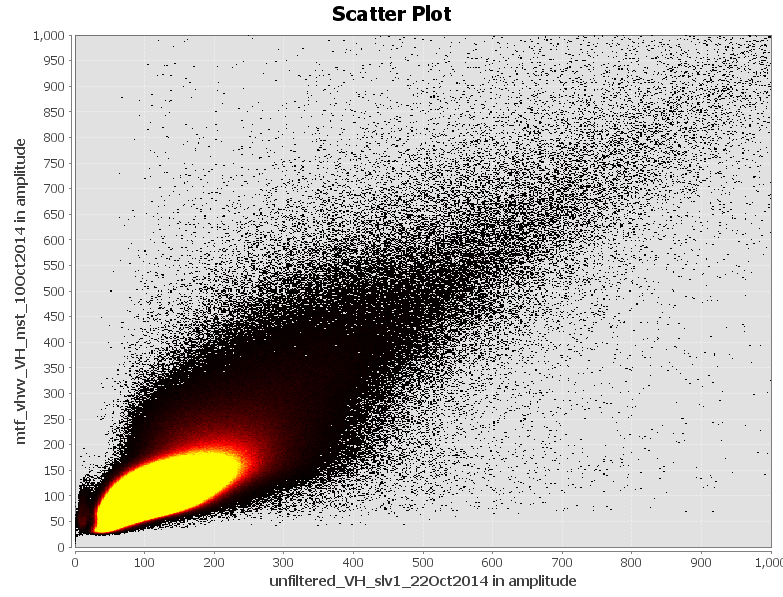
unfiltered VH vs. single-polarization filtered VH
unfiltered VH vs. dual-polarization filtered VH
They are similar to a large degree.
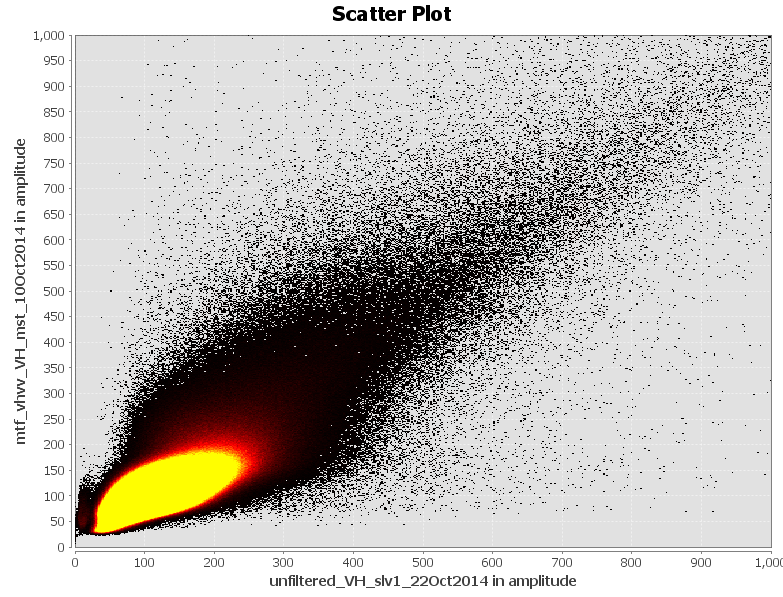
single-polarization filtered VH vs dual-polarization filtered VH
So there are differences in the image, but we can’t tell if they are drastic.
So, let’s have a closer look at some areas. I tried to select areas with various land use types.
1.unfiltered
2. single-polarization filtered VH
4. dual-polarization filtered VH
Visually, some changes can be observed, but their impact is small. Due to the double number of input data sets the product of the dual-polarization filter is a bit smoother.
It surely depends on the application. Working with polarimetric signatures of the VH/VV Sentinel-1 IW mode I would personally disadvise filtering with both polarizations at once. But for simple image analyses, thresholds, classifications I can’t find any harm in doing it.
Any suggestions for further tests?